Remarques sur différents mouvements
Une analyse détaillée et très précise de ce mouvement a été publiée par Herman Sabbe [1]. Il décrit cette pièce comme une collection de règles qui contrôlent plusieurs processus se déroulant sur sept niveaux différents. Ceci porte sur les « paramètres » suivants : la hauteur des sons et les diverses classes de hauteurs, la durée ou la distance séparant les entrées, la dynamique, la transparence et le timbre, l’écriture et la forme globale. Afin de pouvoir décrire le tournant dans l’œuvre causé par l’effet alarmant produit par le do♯4 retentissant, Sabbe se réfère à la théorie des catastrophes développée par René Thom (qui est une branche de la théorie des bifurcations), « caractérisée par une complémentarité des fluctuations soudaines à l’intérieur d’un système, et par la fonction perpétuante du même système qui réside dans les changements de valeur discontinus » [2].
Nous ne voudrions pas ici attaquer le fond de cette analyse mais plutôt apporter quelques ajouts, corriger certains détails et surtout mettre d’autres accents. Ainsi on peut se demander si la notion d’« activité mélodique » [3] de Sabbe ne peut être révisée, si par exemple il n’est pas préférable de différencier entre des intervalles séparés par un silence et ceux qui, grâce au jeu legato et à une emphase causée par un crescendo, forment les phrases mélodiques minimales. Sabbe affirme par exemple qu’à la mes. 11, la clarinette réalise grâce à la sixte mineure mi2– do3 un maximum d’activité mélodique [4]. Or ce mi2 est la note finale d’un crescendo, alors que le do3 commence la phrase suivante. Hugo Riemann a introduit pour ce type d’intervalles la notion « d’intervalle mort » [5] et on peut supposer qu’aussi dans cette pièce, les intervalles séparés par une césure seraient sans pertinence mélodique. Plutôt ils seraient plutôt liés au geste mélodique emphatique connu de la musique traditionnelle.

Exemple 1a : Ligeti, Dix Pièces, no 1, commencement (en do). Séquence des sons mf (avec le son rattaché): si (la#) – mi (fa#) – fa (mi) – la (si) – sol (lab) – la (si) –fa (mib) – sol (la) – si (do) – sol# (fa#) – sol (la) – (etc.)
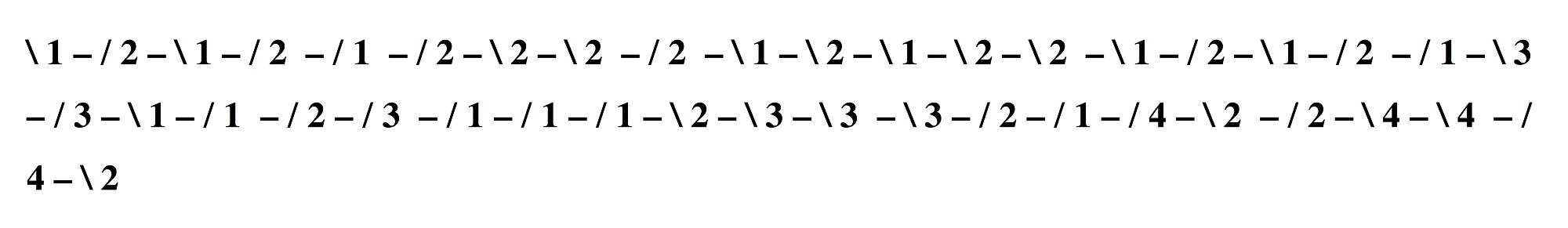
Exemple 1b : Pièce 1, mes. 2-14, intervalles mélodiques après les crêtes mf ( / = ascendant, \ = descendant, 1 = seconde mineure, 2 = seconde majeure, 3 = tierce mineure, 4 = tierce majeure)
Comme on le voit dans l’exemple 1a chacun des instruments jouent des crescendos de pp à mf pour revenir aussitôt à pp. Le geste mélodique, qui s’entend même à l’intérieur du cluster de cinq sons grâce à son caractère gestuel marqué, se termine quand on en arrive au maximum de la dynamique (voir dans l’exemple 1a les lignes qui relient ces maximums). En revanche, les « intervalles morts » disparaissent dans la texture des accords de cinq sons et sont mélodiquement inopérants. Toute la première section de cette pièce (mes. 2-14, exemple 1b) est constituée par ces gestes mélodiques en crescendo [6]. Ligeti s’arrange pour que les mouvements mélodiques s’élargissent vers la fin, allant jusqu’à la tierce majeure (4) réalisée pour la première fois mes. 12. Ainsi, en prenant en considération exclusivement les intervalles mélodiques, on confirme exactement le résultat que Sabbe obtient en les considérant tous (mélodiques ou « morts ») : l’élargissement des intervalles est un élément du processus d’augmentation de la tension qui marque cette première section [7].
Sabbe ne se préoccupe aucunement de la structure des accords de cinq sons qui déterminent les changements de couleur harmonique dans la première section. Il se concentre sur la « conquête » progressive de l’espace de douze sons en soulignant à juste titre le fait que la classe de hauteurs do♯ (mes. 16), d’abord discrète, fait ensuite une entrée spectaculaire : « La rotation permanente des onze hauteurs engendre en fait la tension qui rendra possible le triomphe de la douzième hauteur » [8]. En vérité, ce ne sont pas onze, mais bien cinq hauteurs qui sont mis en « rotation » à la fois. En partant du cluster « diatonique » de cinq sons du début (que l’on peut qualifier de phrygien grâce à son agencement mi–fa–sol–la–si) le compositeur forme, en changeant les hauteurs dans une partie [9], des accords de cinq sons toujours différents qui ont leur caractère propre, ou plutôt leur couleur harmonique spécifique, comme dit Ligeti : « L’harmonie et les intervalles sont traités ici comme s’il s’agissait de timbres » [10]. Par exemple, le cluster phrygien sur mi2 à la mes. 2, qui paraît un peu sombre, s’éclaircit progressivement en passant à travers différentes phases intermédiaires avant d’aboutir à un cluster ionien sur mi2 (mi–fa♯–sol♯–la–si) à la mes. 4 (voir exemple 2). Des 117 accords de cinq sons qui apparaissent en l’espace de 13 mesures (mes. 2-14) très peu ont une structure intervallique identique et parmi ceux-ci un soupçon seulement présente le même degré de transposition ; voir ici un résumé systématique de tous les accords de cinq sons : [11].

Tableau 2 : Pièce 1 (structure des harmonies en ordre systématique)
Les clusters de tons entiers (2222), qui apparaissent tous deux mes. 9, ou les clusters de demi-tons (1111) que l’on entend dans les mes. 12 (sur sol♭) et 14 (tous deux sur mi♭), ou encore diverses clusters diatoniques peuvent être considérés comme accords « remarquables ». Cependant, la plus grande majorité de ces accords sont de forme libre, c’est pour cette raison que les modèles plus connus ne ressortent pas. C’est la variété qui prédomine et donc le chatoiement de la couleur harmonique.
Ce qui est important d’autre part est l’organisation des hauteurs extrêmes qui forment un cadre fixe (ré2–do3) à l’intérieur duquel des tendances et mouvements importants ont lieu. Ainsi l’élargissement vers le haut de l’ambitus initial (mi2–si2) est atteint après déjà quelques mesures (do3 mes. 5), alors que celui vers le bas n’aboutit qu’à la mes. 7 (ré2). Jusqu’à la mes. 14 on retrouve toujours l’intervalle de septième mineure dans des accords isolés de cinq sons, puis à la fin de la première section de plus en plus compressé, tout d’abord dans un intervalle de tierce majeure (1111), puis dans la mes. 15 dans son extension minimale sous forme d’une tierce mineure remplie mélodiquement (111). Pour de ne pas être obligé de compter l’addition de chaque nouvelle note de la cinquième à la onzième afin de remarquer l’entrée de la douzième, les accords de cinq sons développent, grâce à l’élargissement de l’intervalle-cadre, une force quasi vectorielle qui se réfère à l’expansion vers le haut (do3–do♯3) et à la fois vers le bas (ré2–do♯2). Le coup de feu du do♯4 qui, comme décrit plus haut, amène un changement de caractère avec son fff soudain, incarne certes la classe de hauteurs attendue, mais non pas l’octave visée. C’est ici que s’applique l’image employée par Ligeti : « … il y a là des particularités formelles, comme le changement soudain, abrupt, d’une case à l’autre de l’échiquier » [12].
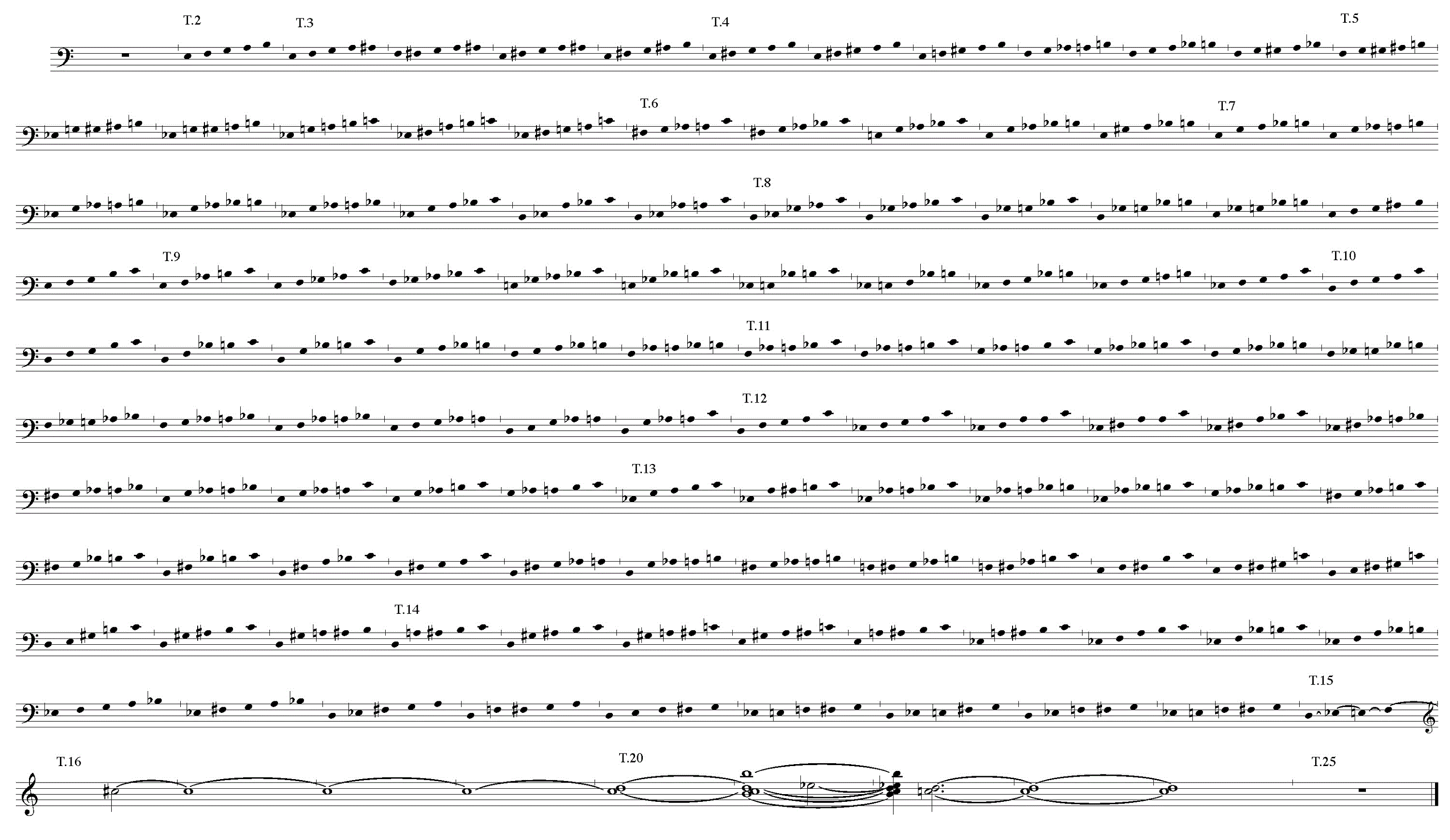
Exemple 2 : Pièce 1 (toutes les harmonies)
La fin de la pièce renverse le processus : là où le son de sirène do♯4 - enrichi entre-temps de dissonances tranchantes [13] - est soudainement « débranché » (mes. 22), nous entendons une implosion sonore. Il nous reste les hauteurs de l’intervalle-cadre de la première section, maintenant transposées à l’octave supérieure (ré4–do4). Mais elles ne sont jouées ici ni « dolcissimo » ou « espressivo » comme au début, mais plutôt dans un timbre terne, « (quasi eco) tenuto, senza vibrato » [14].
Dans ses analyses Sabbe a très justement signalé les données psychoacoustiques qui jouent un rôle important dans l’écoute de beaucoup d’œuvres de Ligeti. Parmi celles-ci figure entre autres le dépassement de ce que l’on nomme le seuil de distinction des sons individuels séparés, causé par la très haute densité d’événements que l’on retrouve, horizontalement, au sein d’une unité de durée dans chaque partie individuelle, et, verticalement, dans la superposition de nombreux instruments ou parties. Dans certaines compositions de Ligeti la division rythmique est conçue de manière à ce que les notes des parties individuelles de la micropolyphonie tombent sur les trous des parties complémentaires, produisant ainsi, par cet interlocking, un quasi-continuum. Cette technique apparaît par exemple dans Atmosphères [15] et Lontano [16] où la perception d’un mouvement temporel en direction d’un but spécifique (au sens d’une « poussée vers l’avant » dynamique) est suspendu. Cause de ce phénomène est d’abord la densité horizontale et verticale des événements émergents ainsi que l’absence d’accents métriques (comme le précise le compositeur, il n’y a pas, par exemple, de mesure perceptible dans Atmosphères). Les auditeurs ont alors l’impression de percevoir les transitions d’une surface sonore statique à une autre.
On a la même impression quand on écoute la première des Dix Pièces pour quintette à vent, en tout cas dans les mes. 1-15, qui (voir plus haut) se présentent comme la transformation progressive du cluster mi–fa–sol–la–si énoncé à la mes. 2 (voir exemple 2). Si l’on peut très bien déchiffrer l’organisation tonale à l’intérieur de chaque partie et celle produite par la superposition des accords en lisant la partition, des problèmes plus redoutables se posent à l’auditeur qui se réfère uniquement à la réalisation sonore de la pièce. Tout d’abord, il est difficile d’isoler, seulement en les écoutant, les voix individuelles au sein d’accords qui sont pressés dans un ambitus restreint. Ensuite, à cause de l’écriture et du mode de jeu prescrit par le compositeur, l’énergie spectrale des instruments se concentre dans une bande de fréquence relativement étroite. L’image sonore est douce et plutôt centrée vers le « milieu », c’est-à-dire que celles des fréquences hautes font en grand partie défaut qui, chez les instruments à anche (ici, clarinette, cor anglais, basson), agissent comme zones formantiques de l’énergie spectrale surtout lorsque les instruments sont joués avec une dynamique adéquate (mf, f, ff). Ligeti varie certes toujours la dynamique au moyen d’une suite de crescendos et de decrescendos (pp < mf > pp) qui comprennent toutes les voix, même si les nuances maximums et minimums ne sont pourtant pas rejointes simultanément. Plutôt, le compositeur a étendu ici à la dynamique son principe de processus contraires-complémentaires qu’il a appliqué dans cette œuvre (comme dans d’autres), et selon lequel la croissance d’une valeur de paramètre dans une partie correspond à sa décroissance dans une autre [17]. La conséquence est ici que même si les arcs des crescendos et decrescendos des voix individuelles - qui ne sont superposés qu’en partie – causent une hausse et une baisse relative du volume de la sonorité produite par l’ensemble des cinq instruments, ces variations de volume n’atteignent pas l’ambitus (en décibels) que l’on obtiendrait si les crescendos et decrescendos s’effectuaient en exacte simultanéité dans les cinq instruments. L’effet qui résulte de ce léger décalage entre les crescendos et decrescendos est que, du point de vue des nuances, l’apport des voix individuelles à l’intérieur de l’accord les montre en fluctuation constante, tandis que la dynamique globale des cinq voix et ainsi le volume des enregistrements de cette œuvre ne présente aucun saut extrême. Cependant, l’ensemble de ce processus de crescendos et de decrescendos sur cinq voix produit au potentiomètre une courbe dynamique légèrement ascendante et descendante.
La transformation uniforme de la dynamique est accompagnée d’une augmentation et diminution des partiels produits par chaque instrument car un jeu plus marqué (passage du pp au mf) dans les instruments à vent veut dire un accroissement de la pression et de la vitesse du souffle d’attaque. Par conséquent, tout accroissement de la dynamique entraîne une augmentation de l’énergie et la densité spectrale. C’est pourquoi la valeur moyenne de la distribution de l’énergie spectrale (le centroïde spectral, calculé à partir des fréquences et des valeurs d’amplitude des sons partiels du spectre [18]) augmente et diminue de façon égale : le nombre et la quantité d’énergie des partiels déterminent en grande partie la croissance et la décroissance constante de la clarté sonore de ces clusters.
Afin de les rendre accessibles à une vérification objective, nous aimerions illustrer les résultats esquissés ici en les soumettant à une analyse sonologique. On trouvera tout d’abord dans l’exemple 3 la hausse et le déclin de la dynamique d’une durée d’environ 50 secondes (mes. 1-11), tiré d’un enregistrement de l’œuvre par le Quintette à vent de la SWF; on voit que le volume sonore de 55 dB du début (calculé comme moyenne quadratique du volume), augmente – avec les crescendos et decrescendos - graduellement presque jusqu’à 70 dB. Le cours de la ligne du volume sonore correspond assez bien à la courbe du centroïde spectral, réalisée à partir du même enregistrement et du même extrait, et que nous reproduisons dans l’exemple 4.
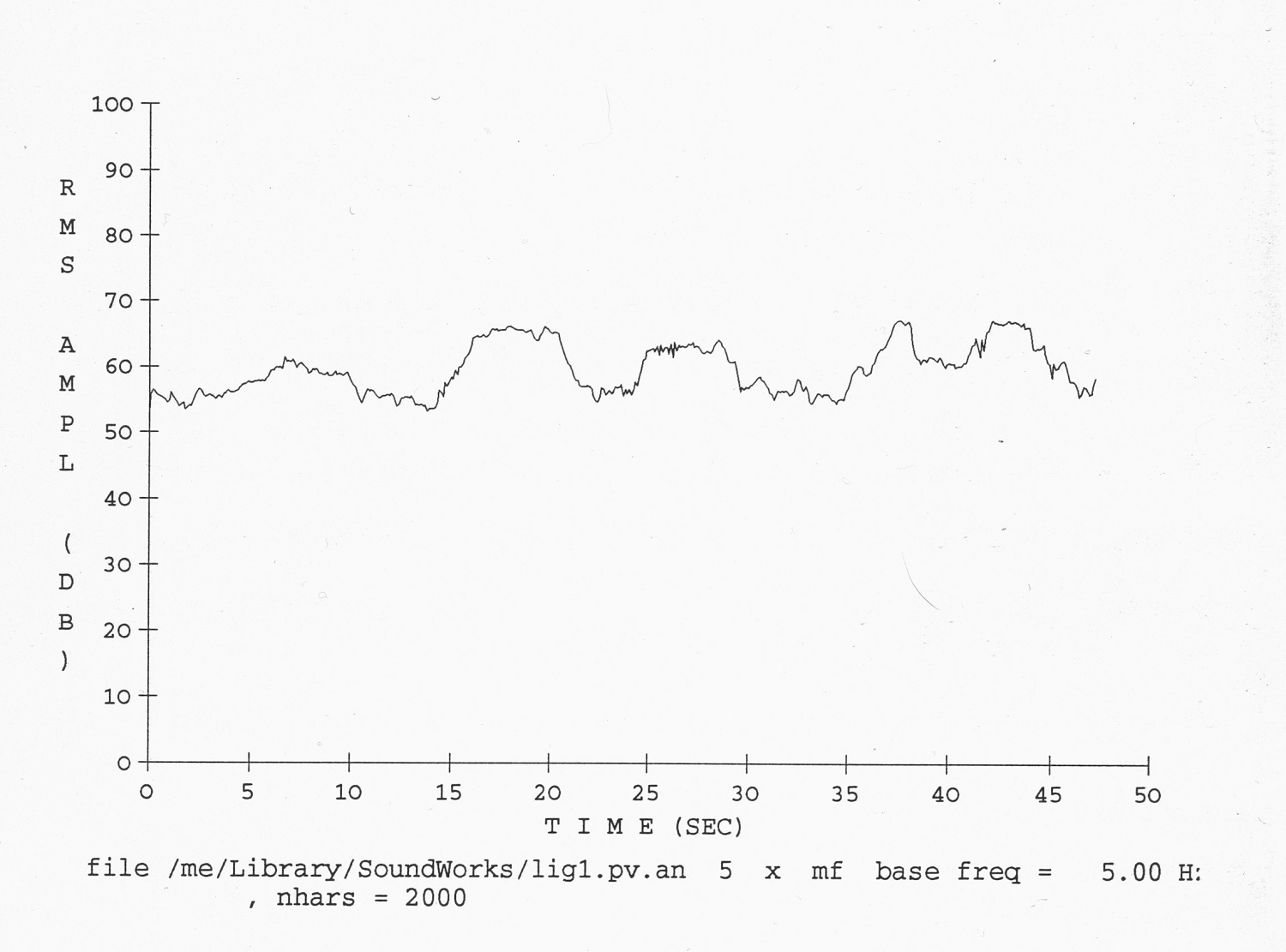
Exemple 3 : Pièce 1, ligne du volume sonore 0''–48'', FFT: 16384, Hamming, Quintette à vent du Südwestfunk Baden-Baden
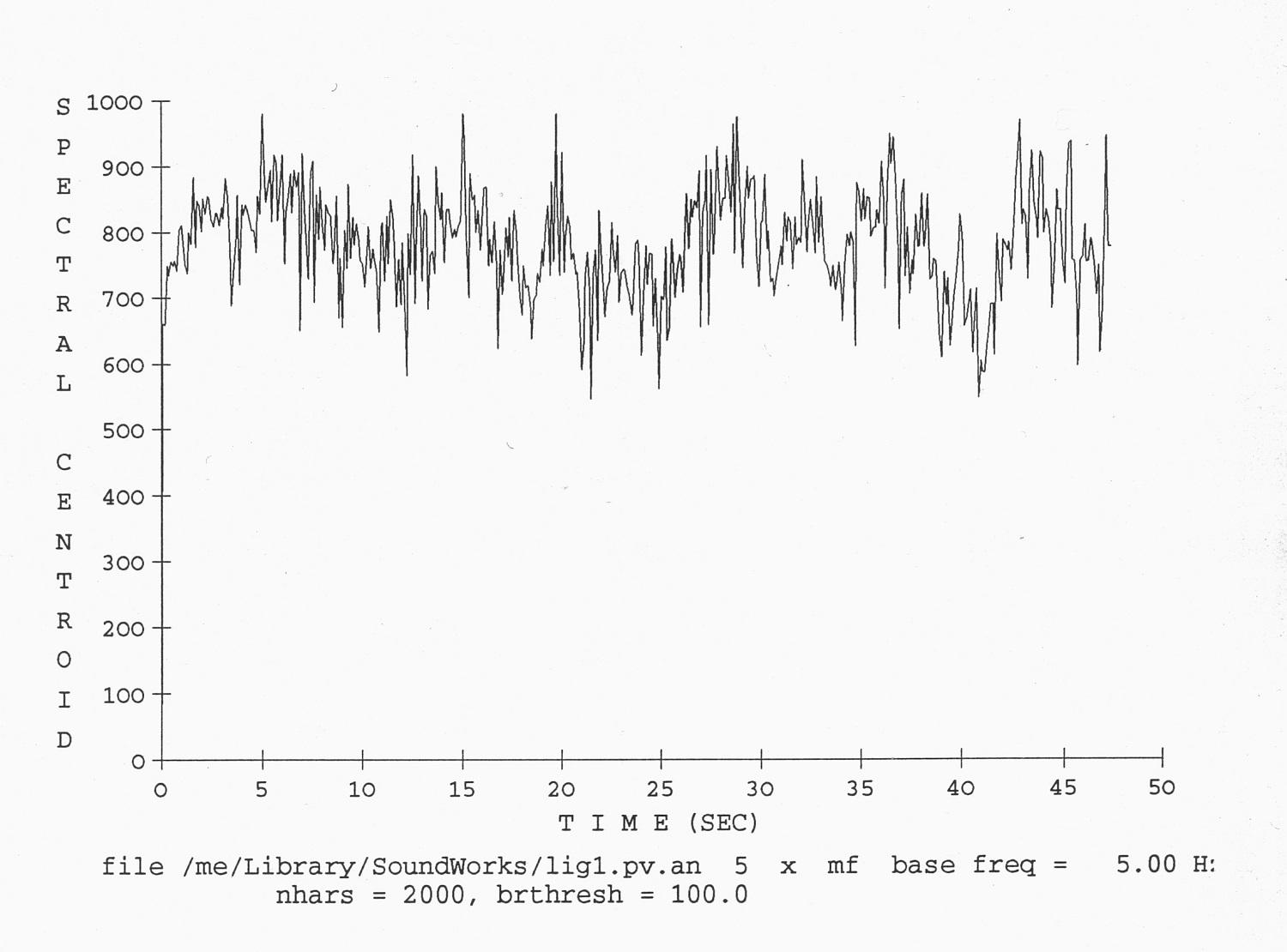
Exemple 4: Pièce 1, courbe du centroïde spectral 0''–48'', FFT: 16384 pts, Hamming
Les arcs de la dynamique causent l’augmentation et la diminution de l’énergie spectrale et la hausse et le déclin des partiels produits par les instruments ressort de l’exemple 5, qui montre une suite de 82 spectres (chacun calculé à partir de 32768 échantillons, ce qui, avec une fréquence d’échantillonnage de 44.1 kHz correspond à une durée sonore d’à peu près 0,7 secondes). Comme les fenêtres de durée des 82 spectres se chevauchent avec un facteur 0, 5, nous représentons ici en vérité à peu près 30 secondes de l’enregistrement de la SWF, à savoir le segment t = 22,5’’ jusqu’à t = 53’’. Dans cet extrait se détachent cinq zones maximum de la distribution de l’énergie spectrale (marqués dans l’exemple par des chiffres romains, de I à V), auxquelles correspondent cinq pics dynamiques causés par des crescendos. Cependant l’exemple 5 montre aussi que ce n’est pas seulement la structure des partiels ou des composantes spectrales qui varie d’un accord à l’autre mais également la structure temporelle de la succession entière des sons est transformée par les entrées des voix individuelles et de la durée toujours différente des notes jouées.

Exemple 5 : Pièce 1, t = 22,5'' ® 53'', FFT: 32768 pts, Hamming, Hop: 0,5, 82 spectres
Ainsi se constitue un entrelacs subtil de voix, un tissage de voix - caractéristique de l’œuvre de Ligeti à la fin des années 1960 - dont la durée et le spectre sonore se superposent. La structure sonore se laisse assez bien représenter objectivement grâce au sonagraphe. Cette manière de représenter la durée et la fréquence a l’avantage à la fois de ressembler à la notation habituelle (qui donne également la dimension de la durée, sur l’axe x, et la fréquence, ou plus exactement le logarithme de la fréquence, sur l’axe y), et de lui être supérieure en ce que le sonagramme ne rend pas uniquement les fréquences fondamentales des sons musicaux (auxquelles se limite la notation traditionnelle) mais fait apparaître également les sons partiels qui en dérivent acoustiquement, avec leurs fluctuations de fréquence et d’amplitude (cette dernière est au moins relativement déchiffrable dans les zones en gris). La spectrographie est donc en effet une sorte d’écriture sonore, quasiment en 3D.
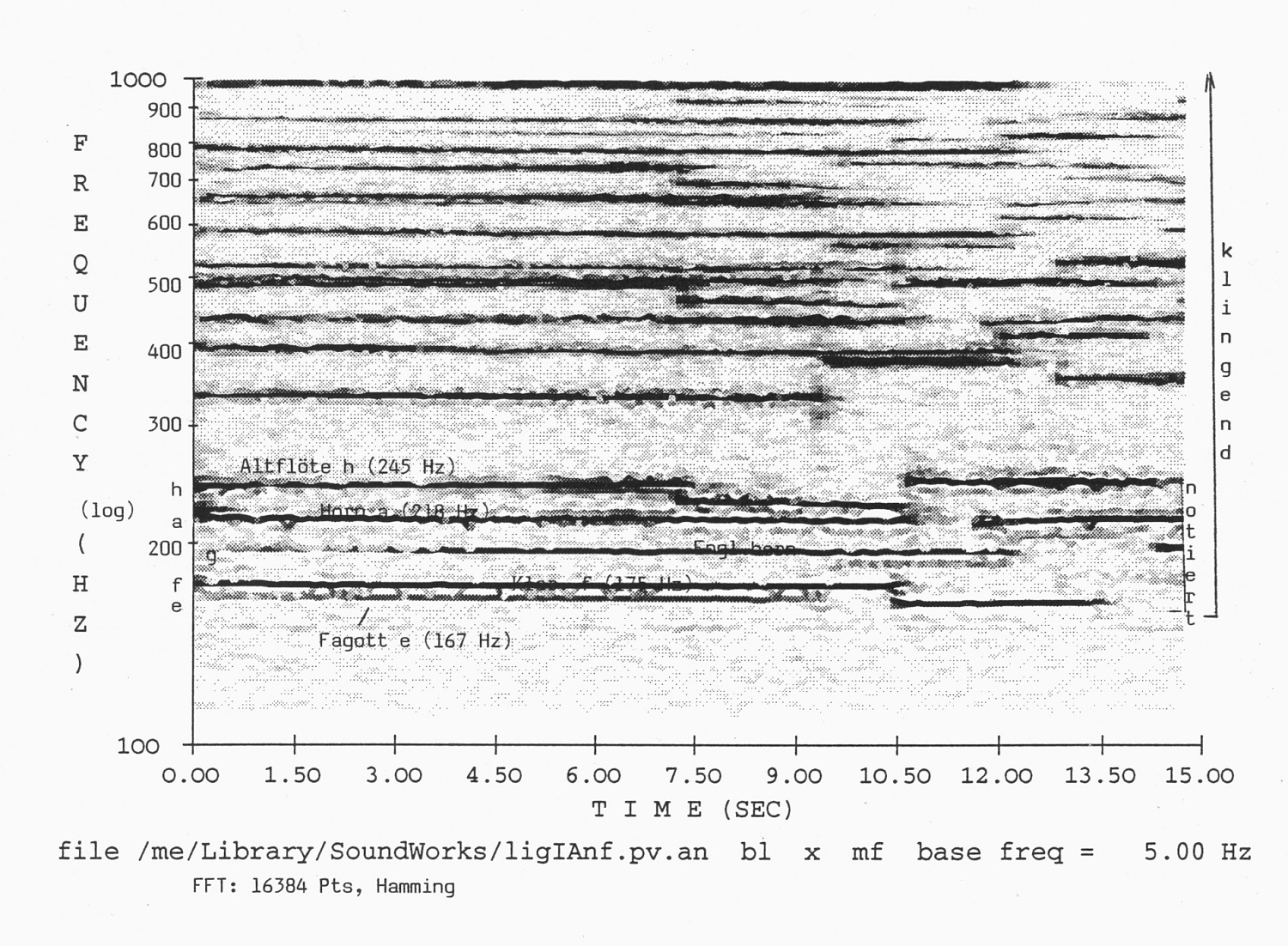
Exemple 6 : Pièce 1 (début), spectrogramme
L’exemple 6 montre 15 secondes du début de la première pièce dans l’enregistrement de la SWF. On y reconnaît à la fois le cluster de départ sur les notes mi–fa–sol–la–si, avec leurs fréquences fondamentales à 167, 175, 196, 218 et 245 Hz (basées sur l’intonation réelle) ainsi que le fait que malgré l’attaque dolcissimo des instruments, l’énergie spectrale augmente dès le début jusqu’à 2 kHz approximativement grâce aux partiels des cinq instruments. Il est vrai que les parts les plus fortes se situent entre 167 Hz et 1 kHz, la zone qui est ici représentée dans ce sonagramme. Les battements audibles produits par des partiels ou composantes spectrales parfois très rapprochés rendent difficile l’analyse auditive du premier accord ainsi que sa transformation causée par de petites progressions mélodiques dans la flûte, puis le basson, ensuite la clarinette etc., après environ 7, 2’’. Ces figures mélodiques très resserrées et une sonorité qui se tient pour l’ensemble dans le registre médian concentrent l’énergie spectrale audible sur une bande de fréquence plutôt étroite.
Si on ajoute à ceci le signal audio d’une analyse selon la méthode du cochléagramme - qui repose sur un système de filtres passe-bande, un peu comme l’analyse des fréquences de notre audition périphérique, et qui représente des patterns de stimulation locaux de la membrane basilaire sur une échelle de 25 groupes de fréquences (nommée échelle de Bark [19]) - on voit que, sur les 20 premières secondes de notre enregistrement, l’énergie spectrale la plus forte tombe dans une bande de fréquences qui regroupe uniquement sept groupes fréquentiels (voir exemple 7). On appelle groupes fréquentiels (ou « seuil critique de la bande passante ») une bande de fréquences qui correspond à une zone continue de stimulation de la membrane basilaire (en mm), au sein de laquelle des composantes spectrales simultanées (selon le contexte) ne peuvent presque plus, ou plus du tout, être différenciées voire encore moins identifiées. Si, comme dans le cas présent, un nombre plutôt élevé de composantes spectrales tombe dans seulement quelques bandes de fréquences, composantes dont les fréquences n’ont entre elles que très peu de rapports harmoniques, il en résulte des accords semblables à des clusters dont la structure interne n’est saisissable qu’avec un peu de pratique.
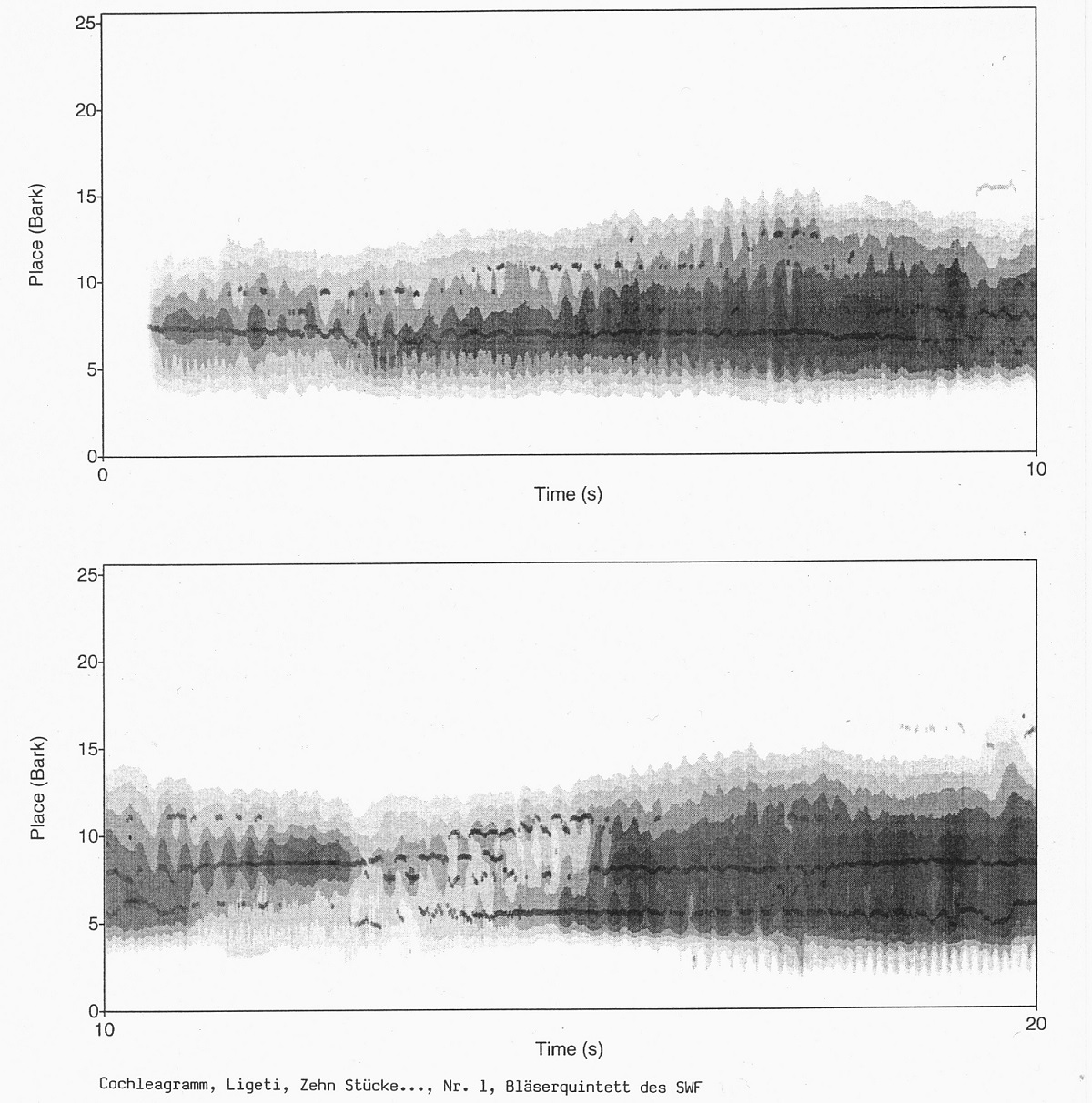
Exemple 7 : Pièce 1, cochléagramme, Quintette à vent de la SWF
Après les transformations du cluster initial décrites plus haut (mes. 1-15), la première des Dix Pièces aboutit,pour ce qui est de sa structure formelle et dynamique, à une sorte de transition (clarinette, cor et basson, mes. 15-16), à laquelle se joint sur la dernière noire de la mes. 16 une troisième partie caractérisée par l’échange d’instruments du registre grave à aigu ainsi que par une dynamique des plus larges possible. Ces deux facteurs font que, dans les mes. 20-21 (voir exemple 2), la dissonance musicale, qui est causée par la friction entre les demi-tons, ressort de façon extrême. L’énergie spectrale (spektrale Hüllkurve) s’étend maintenant jusqu’à presque 10 kHz (exemple 8, dans l’enregistrement des London Winds) ; les indications de jeu exigées ici (fff, tutta la forza) dans la flûte alto, le cor anglais etc. sont à l’origine des composantes bruitées dans le son produit par les instruments.
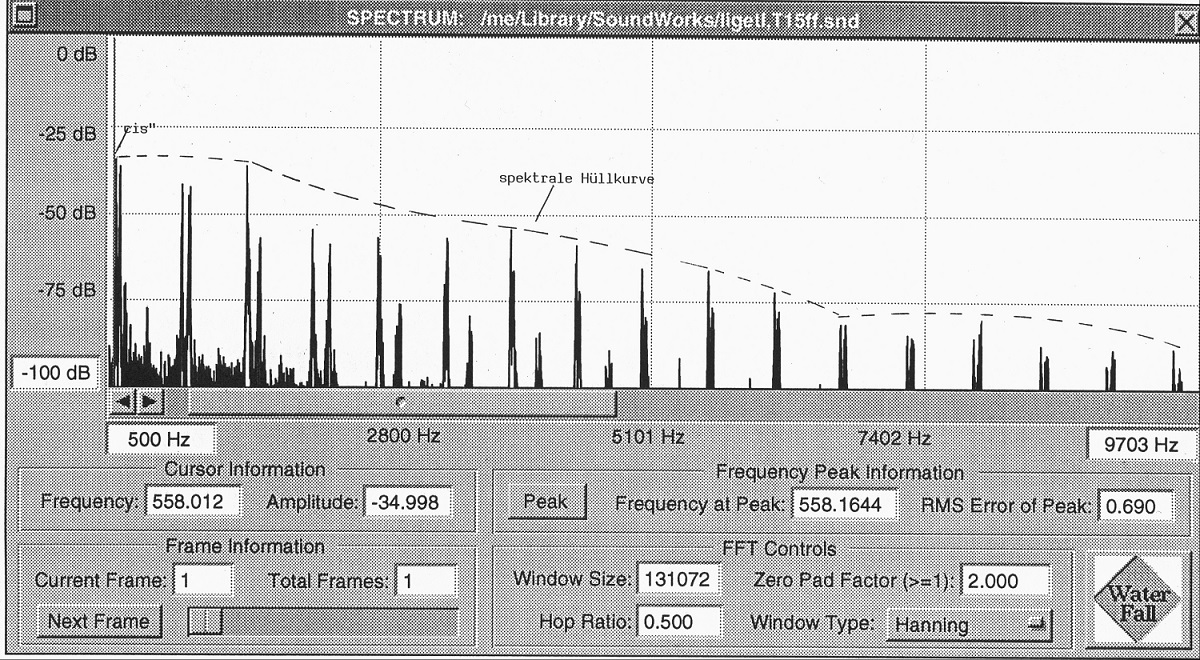
Exemple 8 : Pièce 1, London Winds
On voit cela clairement dans le spectrogramme plus long (131072 échantillons = 2,97’’ de musique) de la mes. 21, quand la flûte alto joue un si4 au-dessus du cluster chromatique do♯4, ré4 et mi♭4 des autres instruments (exemple 9). Alors que leur intonation reste assez stable dans l’extrait considéré, la fréquence de base de la flûte alto parcourt une zone de fréquences plus grande (de 990 à 1016 Hz à peu près), même si la fréquence de base exigée - si4 - est clairement trop aiguë.
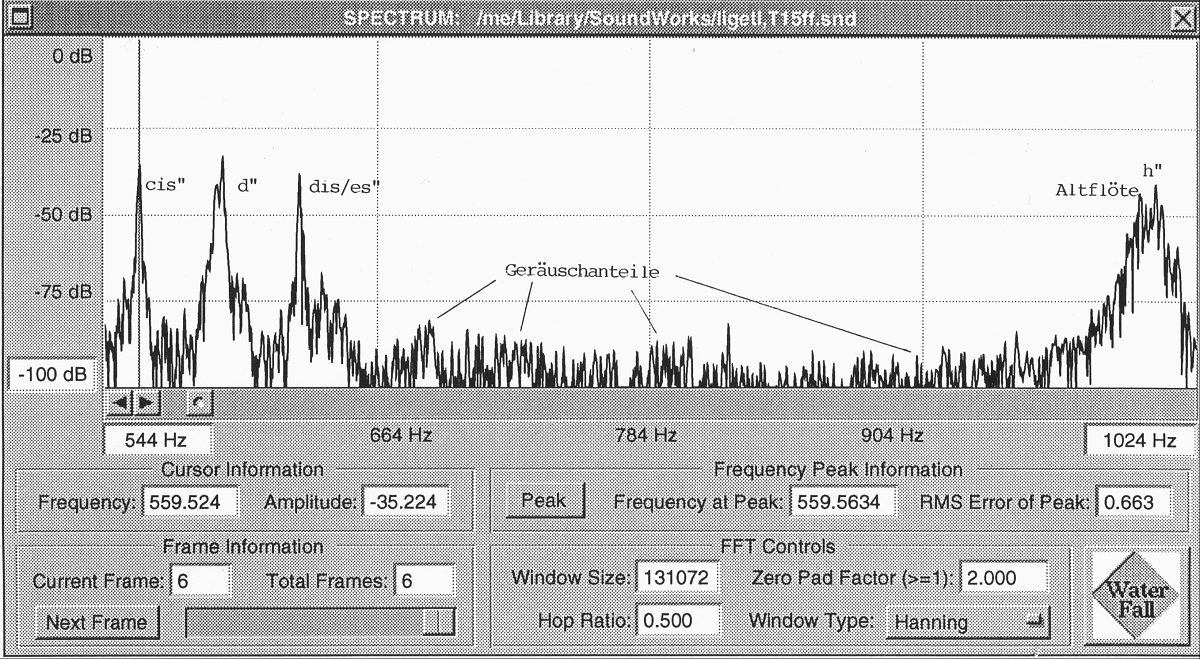
Exemple 9 : Pièce 1, mes. 21, London Winds