texte

Le terme « profilème » vient de ce que ces entités correspondent aux unités distinctives fondamentales lorsque le MTP est le signifiant des UST. C’est-à-dire qu’ils jouent dans le MTP le même rôle que les lettres dans le mot : ils ne sont pas porteurs de signification temporelle en eux-mêmes, mais servent à opposer et distinguer les UST qui, elles, portent la signification (tout comme le font les lettres « m » et « p » dans la distinction entre les mots « mort » et « port »).

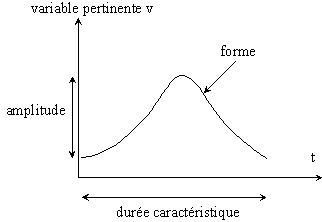
Un profilème est constitué d’une fonction temporelle élémentaire affectant une variable pertinente donnée. Nous avons vu que les fonctions temporelles ne décrivent que l’allure de l’évolution temporelle de la variable pertinente. Cette allure peut tout naturellement être visualisée sous la forme d’un graphe fonctionnel ou par des symboles conventionnels.

Le graphe du profilème contient, en plus de l’indication de forme, deux informations discriminantes qui complètent l’écriture symbolique de la formule. Ces informations sont la durée caractéristique et l’amplitude des variations. Ce dernier paramètre n’a pas encore été étudié, mais les analyses dans le domaine du visuel nous incitent à penser qu’il est pertinent dans la perception de l’UST, à savoir qu’une variation trop grande de la variable pertinente peut détruire l’UST. La valeur exacte de la durée caractéristique d’un profilème n’a pas d’importance dans le domaine sonore. Toutefois les UST se différencient selon deux types de profilèmes : les courts et les longs. Un même profilème peut correspondre à deux UST différentes selon qu’il est de durée courte ou longue, bien qu’il concerne la même variable pertinente (cas des UST Obsessionnel et Par vagues, par exemple).

En plus des paramètres mentionnés, le sens de variation pour les fonctions monotones peut être pertinent dans une UST, mais parfois il ne l’est pas (pensons par exemple à l’UST de type Trajectoire inexorable, dans le domaine des fréquences, qui peut évoluer vers le grave ou l’aigu). Pour la représentation graphique de tels profilèmes, nous avons choisi, par convention, de dessiner une flèche à chacune des extrémités du trait représentatif de la forme.

Les profilèmes permettent également de décrire des fonctions périodiques et pseudo-périodiques. Afin de ne pas compliquer les schémas par la reproduction de la forme sur plusieurs périodes, on utilise la représentation mathématique des fonctions périodiques à l’aide du peigne de Dirac : toute fonction périodique peut être décrite comme la convolution d’une forme élémentaire avec un peigne de Dirac dont la période est celle de la fonction périodique. Un peigne de Dirac n’est rien d’autre qu’un pic qui se répète de façon périodique. La convolution a pour effet de remplacer le pic par la forme centrée sur la position du pic. Le modèle intègre donc un profilème « peigne » qui n’apparaît jamais individuellement mais qui entre dans la composition des profils périodiques.

Enfin, il s’avère utile de décrire une fonction temporelle erratique mais qui peut être associée à une structure signifiante (par exemple, une séquence élémentaire de notes dont le contour mélodique n’a pas d’importance en soi). Ce profilème a été dénommé une « séquence ». Il représente un geste (trait musical ou graphique) qui n’a pas, en lui-même, de comportement temporel orienté mais qui, combiné à d’autres profilèmes, peut entrer dans la composition d’une UST.

Avec ces conventions, les profilèmes entrant dans la constitution des UST musicales sont au nombre de 13 et se répartissent selon 4 familles en fonction de leur forme. On peut sans aucun doute en augmenter le nombre : le principe de construction de ces profilèmes est simple et il sera facile de les inclure dans de nouveaux MTP. Néanmoins, compte-tenu de leur grande généralité, les profilèmes répertoriés permettent déjà de bâtir, par combinaison, un très grand nombre de motifs. Ils ont été suffisants pour décrire tous les exemples sonores avec lesquels nous avons travaillé.

Les profilèmes de forme constante

La famille des profilèmes de forme constante comporte trois représentations. Le plus courant est le plat, noté Pl. Il s’agit d’une fonction dont la valeur peut fluctuer (et même, localement, dans des proportions importantes), mais qui est globalement perçue comme à peu près constante. Dans les UST, elle est souvent utilisée lorsque le comportement temporel n’intervient pas de manière significative. C’est en quelque sorte le profilème « neutre » du système.

La constante, notée Cst, correspond à une valeur rigoureusement constante dont la valeur n’importe pas, à condition qu’elle soit non nulle sur la durée du profilème (c’est, par exemple, une tenue en fréquence). La notation S a été ajoutée au trait pour la différencier du plat.

La constante de valeur nulle, notée 0, est la seule dont la valeur soit distinguée. Le trait horizontal de son graphe est décalé de l’axe des temps et le symbole 0 ajouté à fins de visibilité. Ce profilème traduit, par exemple, un silence pour la variable intensité.


Pl	Cst

0

Figure 2 : profilèmes de forme constante

Les profilèmes de forme monotone

Les profilèmes de la famille des formes monotones sont caractérisés par leur sens de variation (augmentation ou diminution) ainsi que par leur courbure. On distingue les profilèmes globalement linéaires, c’est-à-dire sans accélération, et les formes courbes pour lesquelles l’accélération est une donnée perçue significative. Cependant, la valeur précise de cette accélération, ainsi que la pente des droites, ne sont pas, en elles-mêmes, des données significatives et ne sont donc pas repérées dans les profilèmes.

Parfois, le sens de variation n’est pas une donnée significative, d’où l’existence des profilèmes L (profilème linéaire) et C (profilème courbe) qui repèrent ces cas de figure. Notons que, lorsque les profilèmes de type L participent à une UST, le sens de variation de la fonction temporelle linéaire n’a jamais d’importance (ce qui n’est pas le cas des profilèmes de type courbe). Les profilèmes L+ et L- n’ont donc été ajoutés que par souci de complétude.


L	C

L+	L-

C+	C-

Figure 3 : profilèmes de forme monotone.

Les profilèmes non monotones en cloche

Les profilèmes non monotones en cloche sont caractérisés par une variation croissante, puis décroissante, de la variable pertinente sur leur durée. Les valeurs de départ et de fin de la fonction n’ont pas d’importance. Par conséquent, le profilème peut démarrer ou finir par une valeur nulle. On pourrait construire la famille réciproque des fonctions monotones en creux, c’est-à-dire celle pour laquelle la fonction commencerait par décroître avant de croître. Il s’avère qu’aucune UST connue n’utilise cette famille, nous ne l’avons donc pas représentée.

Deux caractéristiques distinguent les profilèmes de la famille des formes en cloche : la forme de la courbe et sa symétrie. Il s’avère que, dans une UST sonore, la forme exacte de la cloche (très large ou affinée) n’a pas d’influence sur la signification. Si, dans d’autres domaines, il s’avère nécessaire de discriminer les fonctions non monotones par leur forme, il sera facile de définir les profilèmes correspondants. Il convient toutefois, dans les UST sonores, de distinguer les profilèmes qui présentent des valeurs non nulles sur une portion significative de leur durée caractéristique et ceux qui sont nuls presque partout. Ces derniers correspondent à des sons très brefs. C’est pourquoi on a distingué le pulse de la courbe en cloche proprement dite.

Très souvent, la dissymétrie du profilème n’intervient pas dans une UST. Dans ces cas, le profilème en cloche générique Cl est utilisé. Ce profilème ne décrit pas seulement des fonctions temporelles de forme symétrique, il décrit toute fonction croissante puis décroissante pour laquelle la forme exacte n’importe pas. Certaines UST nécessitent toutefois de discriminer les fonctions temporelles présentant un front montant plus raide que le front descendant ou l’inverse. On utilise alors respectivement les profilèmes Cl+ et Cl-.


Π	Cl

Cl+	Cl-

Figure 4 : profilèmes non monotones en cloche

Les profilèmes à fonction exotique

Cette famille comprend le peigne pD et la séquence élémentaire Séq qui ont déjà été présentés.

La représentation de la séquence élémentaire est purement conventionnelle, la séquence pouvant être n’importe quel comportement temporel autre que ceux décrits par les autres profilèmes. Toutefois, dans les motifs composés formés par association, on peut trouver une séquence non élémentaire représentant un comportement temporel quelconque, y compris l’un de ceux représentés par un autre profilème.

Le peigne porte l’indication de la période T et du motif Me. Il intervient dans la représentation des profils de fonctions périodiques ou pseudo-périodiques. Dans les UST, la valeur exacte de la période n’a pas d’importance (ce qui compte, c’est sa valeur relative), ni le nombre de périodes effectivement présentes dans l’événement perçu. L’indication « Me » semble redondante avec le trait vertical pour noter le caractère périodique de la fonction, mais nous verrons que cette redondance disparaît dans les profilèmes pseudo-périodiques. Dans les formules, les ordres de grandeur de T (à savoir T0, T1…) ainsi que les indications éventuelles relatives à T et Me pour les profils pseudo-périodiques seront indiqués entre parenthèses.


pD	Séq

Figure 5 : profilèmes à fonction exotique

Description du modèle

Caractéristiques générales des profilèmes